Go und Mathematik
Kombinatorische Spieltheorie: Eine Anwendung
Jörg Bewersdorff
In den letzten Jahren wurden auf dem Gebiet der kombinatorischen Spieltheorie große Fortschritte erzielt. Dabei gelang es auch, diese mathematische Theorie auf das Go-Spiel anzuwenden und zwar vor allem auf weit fortgeschrittene Endspiele. Praktische Tests erfolgten unter anderem durch eine Implementation der entsprechenden Algorithmen in Spielprogramme. Damit wurde zugleich ein kleiner Beitrag dazu geleistet, Spielprogramme für Go mittelfristig ebenso spielstark zu machen, wie das bei Schach bereits heute der Fall ist. Nicht zu unterschätzen sind aber auch die prinzipiellen Erkenntnisse, die sich über frühere Spielstadien gewinnen lassen, in denen die weitgehenden Voraussetzungen der Theorie meist nur ansatzweise erfüllt sind. Im folgenden werden die grundlegenden Ideen der kombinatorischen Spieltheorie am Beispiel des Go dargestellt.
Dieses Manuskript entstand im Zuge der Vorbereitungen zu meinem Buch "Glück, Logik und Bluff: Mathematik im Spiel - Methoden, Ergebnisse und Grenzen" (siehe Homepage), in dem u.a. die Entwicklung der der kombinatorischen Spieltheorie ausführlich beschrieben wird .
Schach und Go sind wohl die beiden Spiele, die weltweit mit dem höchsten intellektuellen Anspruch gespielt werden, was sich nicht zuletzt in einer Fülle von Fachbüchern und -zeitschriften äußert, in denen die verschiedensten Spielsituationen analysiert werden. Im Vergleich zu Schach ist der Charakter des Go stärker mathematisch geprägt. Insbesondere entspricht die über das ganze Spielfeld vorgenommene Punktwertung im wesentlichen einem Flächeninhalt. Aber auch Stein-Ketten und umschlossenen Gebieten liegen elementare mathematische Sachverhalte zugrunde. Go "hat eine durchgehendere Logik als das Schach, ist ihm an Einfachheit überlegen und steht ihm, glaube ich, an Schwung der Phantasie nicht nach", bemerkte der Schachweltmeister und Mathematiker Emanuel Lasker in seinem Spielebuch "Brettspiele der Völker". Lasker, der dem Go in seinem 1931 erschienenen Buch immerhin achtzig Seiten widmete, war ein starker Förderer des Go. Als Schachweltmeister amtierte er von 1894 bis 1921, als Mathematiker wurde er durch algebraische Untersuchungen von Polynomen mit mehreren Variablen bekannt.
In der letzten Phase des Endspiels unterteilen oft Ketten nicht mehr schlagbarer Steine das Spielfeld in mehrere Teilgebiete. Die weiteren Zugmöglichkeiten innerhalb jeder solchen Teilposition sind dann unabhängig von der Entwicklung auf dem restlichen Spielfeld. Außerdem ergibt sich am Schluß das Spielergebnis als Summe der in den Teilpositionen erzielten Punktwertungen. Daher erscheint es zumindest prinzipiell möglich, Züge lokal in der betroffenen Teilposition darauf untersuchen zu können, wie gut sie sind. Gelingt das, kann die Suche nach einem guten Zug entscheidend vereinfacht werden, weil gegenüber einer Gesamt-Analyse innerhalb der Teilpositionen wesentlich weniger Zugvarianten untersucht werden müssen. Ein sehr einfaches, zwei Teilpositionen umfassendes Beispiel zeigt das erste Diagramm. Wie auch bei allen folgenden Diagrammen werden alle am Diagramm-Rand dargestellten Steine als "lebend", das heißt nicht mehr schlagbar, angenommen. Beim nicht abgebildeten Rest des Spielfeldes wird zunächst davon ausgegangen, daß dort kein sinnvoller Zug mehr möglich ist:
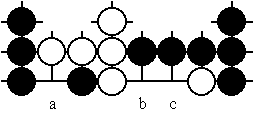
In welcher Reihenfolge sollten die beiden Spieler ihre Steine auf die noch freien, mit a, b und c bezeichneten Schnittpunkte setzen? Wir untersuchen die wenigen Zugmöglichkeiten zunächst insgesamt. Unterschieden danach, ob Schwarz oder Weiß den nächsten Zug machen darf, ergeben sich bei beidseitig gutem Spiel die folgenden Endpositionen:
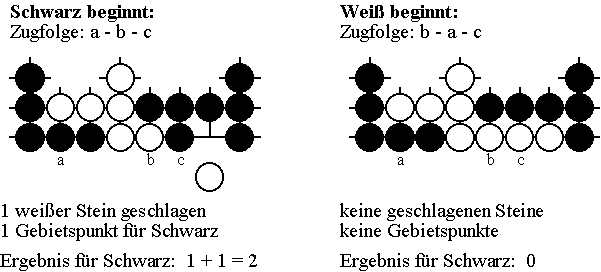
Keiner der beiden Spieler kann durch andere Züge ein für sich günstigeres Ergebnis erzwingen. Es handelt sich um sogenannte Minimax-Strategien, wie sie erstmals der Mathematiker Ernst Zermelo 1912 in einem Referat über "Eine Anwendung der Mengenlehre auf die Theorie des Schachspiels" vor dem 5. Internationalen Mathematikerkongreß in Cambridge als typische Eigenschaft von Zweipersonen-Brettspielen wie Schach und Go dargelegt und nachgewiesen hat. Danach sind die Gewinnaussichten, die wir auch weiterhin immer aus der Perspektive von Schwarz bewerten, in jeder Spielsituation durch einen exakten Wert bestimmt, den sogenannten Minimax-Wert. Ein Gewinn in mindestens dieser Höhe - Verluste werden als negative Gewinne gewertet - kann Schwarz aus eigener Kraft unabhängig von der Spielweise von Weiß erzwingen. Gleichzeitig ist es aber dem Gegenspieler Weiß möglich, so zu spielen, daß Schwarz höchstens den Minimax-Wert als Gewinn erzielen kann. Folglich gibt es in jeder Situation für jeden Spieler mindestens einen objektiv besten Zug. Psychologische Einschätzungen darüber, welche Angriffe der Gegner wohl plant, sind völlig überflüssig. Verhalten sich beiden Seiten in diesem Sinne optimal, dann steht bei Brettspielen wie Schach und Go das Ergebnis von vornherein fest. Jede Position, selbst die Anfangsposition, ist also theoretisch genauso eindeutig analysierbar wie eine Problemposition. Allerdings ist es völlig unbekannt, welche konkreten Gewinnaussichten komplizierte Spiele wie Schach und Go zu Anfang bieten. Insofern eignen sich diese Spiele auch weiterhin bestens für intellektuelle Wettkämpfe. Enden mehrere Partien eines solchen Spiels mit unterschiedlichen Resultaten, dann ist das ein eindeutiger Beweis dafür, daß fehlerhaft gespielt wurde - von wem und in welcher Partie auch immer.
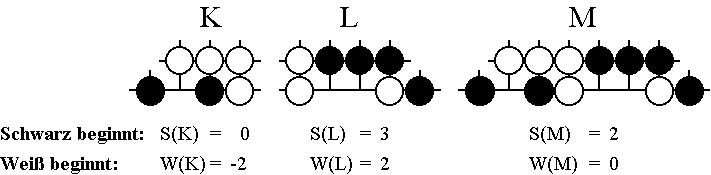
Sieht man einmal vom Sonderfall der Kos ab, wird beim Go eine Spielsituation durch die Position, das heißt die Konfiguration der Spielsteine, sowie durch das Recht des nächsten Zuges vollständig bestimmt. Zu jeder Position G gehören damit zwei Minimax-Werte, die nach dem jeweils beginnenden Spieler mit S(G) und W(G) bezeichnet werden. Das heißt, die Gewinnaussichten von Schwarz betragen, je nachdem ob er anzieht oder nicht, gleich S(G) beziehungsweise W(G). Für die oben untersuchte Position sowie die beiden darin enthaltenen Teilpositionen ergeben sich zum Beispiel die folgenden Minimax-Werte:
Welche Aussagen können nun über die Minimax-Werte einer Position gemacht werden? Grundsätzlich ist der "schwarze" Minimax-Wert S(G) nie kleiner als der "weiße" Minimax-Wert W(G); es gilt also stets die Ungleichung
S(G) > W(G).
Der Grund ist klar: Ein Zugrecht beim Go kann nie von Nachteil sein. Sollte es wirklich einmal keinen vorteilhaften Zug geben, so kann man auf seinen Zug verzichten. Wie vorteilhaft das Zugrecht bei der Position G ist, dafür ist die niemals negative Differenz S(G) - W(G) ein Maß. Sollen die Gewinnaussichten nicht davon abhängen, wer zuerst ziehen darf, kann man die Differenz durch eine entsprechende Zahl von Punkten ausgleichen, die der Nachziehende erhält. Ein solcher Ausgleich ist beim Go im Rahmen einer Gesamtpartie wohlbekannt. So erhält der Nachziehende meist 5½ als Komi bezeichnete Ausgleichspunkte.
Wie schon die Bezeichnung vermuten läßt, können Minimax-Werte dadurch berechnet werden, daß man die auf Schwarz bezogenen Gewinnaussichten abwechselnd maxi- und minimiert. Um etwa den Minimax-Wert S(G) einer Position G zu bestimmen, muß man diese Position unter der Voraussetzung untersuchen, daß Schwarz zuerst zieht. Wie aber wird sich Schwarz verhalten? Was kann er bewirken? Zieht er zu einer Position G', so werden seine weiteren Gewinnaussichten - nun in der Rolle des Nachziehenden - durch den Wert W(G') charakterisiert. Um möglichst viel zu gewinnen, wählt Schwarz also am besten den Zug aus, mit dem der größtmögliche Minimax-Wert W(G') erreicht wird. Dann und nur dann ist sein Zug optimal. Nur so gibt Schwarz nichts von seinen Gewinnaussichten preis, das heißt S(G) ist gleich dem größten W(G')-Wert. Für das Beispiel der Positon M betragen die Gewinnaussichten für Schwarz je nach Zug 2, 1 beziehungsweise 0 und damit im bei optimaler Spielweise 2:
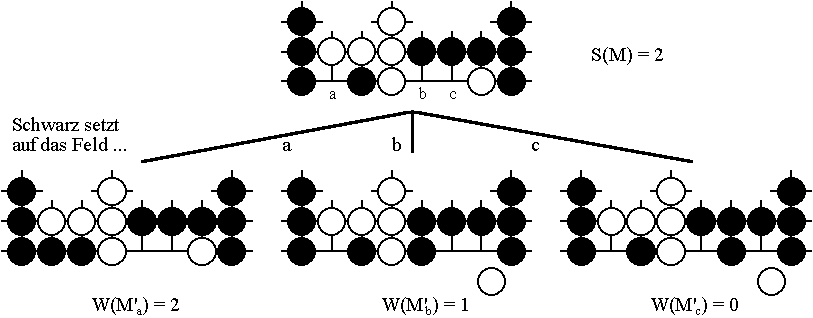
Ist umgekehrt Weiß am Zug, versucht dieser, den Gewinn von Schwarz möglichst klein zu halten. Weiß entscheidet sich daher am besten für den Zug, mit dem eine Position G" erreicht wird, deren Minimax-Wert S(G") möglichst klein ist, das heißt mit dem Schwarz als Nachziehender die geringsten Gewinnaussichten besitzt. Da die beiden Spieler abwechselnd ziehen, lassen sich die Minimax-Werte dadurch berechnen, daß abwechselnd maxi- und minimiert wird. Solche sogenannten Minimax-Verfahren liegen in verfeinerter Form auch allen Spielprogrammen zugrunde, wobei die Gewinnaussichten wegen der beschränkten Rechenzeit nach einer bestimmten Zuganzahl abgeschätzt werden.
| Minimax und Spieltheorie Allgemein sind Minimax-Prinzipien ein grundlegender Bestandteil der sogenannten Spieltheorie, einer mathematischen Disziplin, innerhalb der ökonomische Prozesse auf der Basis von Spielen modelliert und untersucht werden. Begründet wurde die Spieltheorie 1944 durch den Ökonomen Oskar Morgenstern sowie den Mathematiker John von Neumann. Neumann, zugleich auch Vater prinzipieller Computer-Architekturen, hatte wesentliche Ideen der Spieltheorie bereits 1926 im Alter von 22 Jahren in einem Vortrag vor der Göttinger Mathematischen Gesellschaft präsentiert. Darin zeigte er unter anderem, daß das Minimax-Prinzip keineswegs auf Brettspiele beschränkt ist. Vielmehr läßt es sich auf alle Zweipersonen-Spiele ausdehnen, bei denen der Gewinn des einen Spielers gleich dem Verlust des anderen Spielers ist. Anders als bei Schach und Go reicht es bei solchen Spielen allerdings nicht, nur stur in Abhängigkeit des eigenen Informationsstandes über die erreichte Spielsituation zu agieren. Vielmehr müssen Entscheidungen, zum Beispiel darüber, ob beim Pokern geblufft werden soll oder ob man beim Kinderspiel "Papier-Stein-Schere" seine Hand als "Stein" zur Faust ballt, zufällig getroffen werden. Nur so läßt sich die Unkenntnis über die gegnerischen Karten beziehungsweise den gleichzeitig erfolgenden gegnerischen Zug bewältigen, wobei sich wieder für beide Seiten eindeutig bestimmte Gewinnaussichten in Form eines Minimax-Wertes ergeben. Dieser Minimax-Wert ist in einer einzelnen Partie als Spielresultat allerdings selbst bei beidseitig fehlerfreiem Spiel keineswegs zwangsläufig, da es sich bei ihm nämlich nur um einen Mittelwert von zufälligen Resultaten handelt. Meistens noch weit weniger determiniert sind Spiele für drei oder mehr Mitspieler und zwar selbst dann, wenn sie wie die meisten Brettspiele einen allseits offenen Informationsstand bieten. Ihr Ergebnis hängt davon ab, welche Spieler bewußt miteinander koalieren oder sich ungewollt Vorteile zuschanzen. Das heißt, der Einfluß der einzeln agierenden Spieler mit dem Ziel, viel zu gewinnen, ist zu beschränkt, als das dadurch eine stabiles, selbst von koalierenden Gegenspielern nicht zu verhinderndes Spielergebnis entstehen könnte. Das dürfte auch der Grund sein, warum in Form intellektueller Wettkämpfe ausgetragene Spiele wie Schach und Go stets Zweipersonen-Spiele sind; bei mehr als zwei Mitspielern bietet sich im wesentlichen nur die Möglichkeit, ein Turnier zu veranstalten, bei denen die direkte Interaktion immer nur zwischen zwei Spielern stattfindet. Der Erforschung der speziellen Eigenschaften von Mehrpersonenspielen war übrigens 1994 der wirtschaftswissenschaftliche Nobelpreis an die beiden Amerikaner John Nash und John Harsanyi sowie an den Deutschen Reinhard Selten gewidmet. |
Entscheidend für eine mathematische Theorie von Go-Endspielen ist die Analyse einer Position auf der Basis der Eigenschaften ihrer Teilpositionen. Wie können aber die Gewinnaussichten sowie optimale Züge für eine Position aus den entsprechenden Daten der Teilpositionen bestimmt werden? Auf einem sehr abstrakten Niveau, das heißt fast ohne direkten Bezug auf das Go, wurden solche Fragen erstmals 1953 vom Mathematiker John Milnor untersucht, einem damals 22-jährigen Doktoranden in Princeton, der später maßgebliche Beiträge zur Topologie lieferte. In seiner zunächst wenig beachteten Veröffentlichung versuchte Milnor zu klären, wie man bei Positionen, die aus mehreren Teilpositionen bestehen, am besten zieht: In welcher Teilposition empfiehlt es sich zu ziehen, und welcher Zug ist dort am besten? Kann ein Zug innerhalb einer Teilposition absolut der beste sein oder hängt das vom Rest des Spielfeldes ab? In dieser Hinsicht höchst einfach lassen sich Positionen untersuchen, die für beide Spieler symmetrisch sind wie zum Beispiel die folgende:

Eine solche Position umfaßt als Teilpositionen eine Position G sowie die dazu komplementäre, mit -G bezeichnete Position, die entsteht, wenn man die weißen Steine durch schwarze ersetzt und umgekehrt. Die zusammengesetzte Gesamtposition, von Milnor als "Summe" G + (-G) bezeichnet, ermöglicht es stets dem nachziehenden Spieler, alle Züge des Anziehenden in der jeweils anderen Teilposition mit vertauschten Farben zu kopieren. Damit kann der Anziehende keinen echten Gewinn für sich erzielen. Da er aber auch gegenüber dem Nachziehenden keinen echten Nachteil haben kann - schließlich könnte er ja auf seinen Zug verzichten - sind beide Minimax-Werte von solchen symmetrischen Positionen gleich 0:
W(G + (-G)) = S(G + (-G)) = 0
Für eine allgemeine Untersuchung gehen wir von einer aus zwei beliebigen Teilpositionen G und H bestehenden Gesamtposition G + H aus. Eine relativ einfache Möglichkeit, die Gewinnaussichten der Gesamtposition abzuschätzen, besteht darin, aus den Optimalstrategien für die Teilpositionen Strategien für die Gesamtposition zu konstruieren - eine Technik, die übrigens schon Lasker im zitierten Spielebuch analog für sogenannte Nim-Spiele anwandte, bei denen derjenige Spieler gewinnt, der den letzten Zug macht (siehe Kasten "Kombinatorische Spieltheorie"). Beginnt Schwarz in der Go-Position G + H, dann ist es Weiß möglich, jeden Zug von Schwarz in der gleichen Teilposition zu kontern, wobei unter Rückgriff auf die Optimalstrategie für diese Teilposition so gezogen wird, als sei der andere Teil überhaupt nicht vorhanden. Gibt es für Weiß in der betreffenden Teilposition keine Zugmöglichkeit, dann paßt er. Mit dieser einfachen Defensiv-Strategie kann Weiß sicherstellen, daß Schwarz als Anziehender höchstens die Summe dessen erzielt, was für Schwarz in den einzelnen Teilpositionen "drin" ist, also S(G) + S(H). Daher gilt stets die Ungleichung
S(G + H) < S(G) + S(H).
Umgekehrt kann Schwarz eine der beiden Teilpositionen auswählen, dort zu Beginn so ziehen, als sei die andere Komponente nicht vorhanden und anschließend so agieren, wie es zuvor für Weiß beschrieben wurde. Dann ist Schwarz ein Gewinn von mindestens W(G) + S(H) beziehungsweise S(G) + W(H) sicher, so diese beiden Zahlen Mindesthöhen für den schwarzen Minimax-Wert S(G + H) darstellen. Mit Hilfe analoger Überlegungen für den weißen Minimax-Wert W(G + H) erhält man insgesamt die folgende Ungleichungskette:
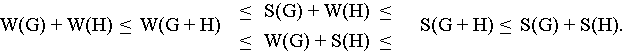
Für das Beispiel der oben untersuchten Positionen G = K und H = L ergeben sich die Werte
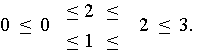
Wie man sieht, sind die Abschätzungen zu grob, als daß es mit ihnen immer möglich wäre, die Minimax-Werte der Gesamtposition aus denen der Teilpositionen zu bestimmen. Das ist auch einleuchtend, wenn man bedenkt, wie einfach die Strategie für die Gesamtposition aus denen der Teilpositionen konstruiert wurde. Insbesondere blieb dabei die schon im Beispiel erkennbare Tatsache unberücksichtigt, daß die Vorteile, die das Zugrecht in den einzelnen Teilpositionen bietet, keineswegs immer demselben Spieler zufallen. Trotzdem lassen sich bereits aus der Ungleichungskette interessante Erkenntnisse ableiten. Dazu empfiehlt es sich, die Ungleichungen in der Form
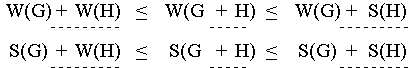
heranzuziehen, da so am besten deutlich wird, wie sich die Gewinnaussichten einer Position G ändern, wenn sie um eine Teilposition H zur Gesamtposition G + H ergänzt wird: Die Änderungen, die beide Minimax-Werte dabei erfahren, werden durch die Minimax-Werte der hinzugekommenen Positionen H begrenzt. Für Schwarz ist daher die Position G + H im Vergleich zur Position G
- mindestens so günstig im Fall von W(H) > 0,
- gleich günstig im Fall von W(H) = S(H) = 0,
- höchstens so günstig im Fall von S(H) < 0 bzw.
- je nach Anzugsrecht und Ausgangsposition G mehr, weniger oder gleich günstig im Fall von W(H) < 0 < S(H).
So grob Milnors Ungleichungen im Einzelfall sein mögen, so wenig können ihre Grenzen im allgemeinen Fall eingeengt werden: Denn zu jeder Position H gibt es spezielle Positionen G (nämlich G = 0 bzw. G = -H), so daß die Minimax-Werte der Position G + H die in den Ungleichungen angegebenen Grenzen annehmen. Insbesondere sind Positionen H mit W(H) < 0 und S(H) > 0 als Teilpositionen isoliert nicht bewertbar, da sie abhängig vom Rest des Spielfeldes die Gewinnaussichten eines Spielers sowohl verbessern als auch verschlechtern können.
Eine Position, bei der beide Minimax-Werte gleich 0 sind und die damit als Teilposition die Gewinnaussichten unverändert läßt, wird Nullposition genannt. Neben den symmetrischen Positionen, wie wir sie schon kennengelernt haben, handelt es sich bei der im nächsten Diagramm abgebildeten Position um eine Nullposition. Warum das so ist, wird später noch erläutert werden.

Ist eine solche Nullposition als Teilposition Bestandteil einer Position, so kann sie ohne Veränderung der Gewinnaussichten ignoriert werden. Damit wird auch verständlich, warum vertraute Symbole wie "+" und "-" verwendet wurden, nämlich weil sie sich mit ihnen in altgewohnter Weise rechnen läßt: So hat die Position G + H + (-H) dieselben Minimax-Werte wie die Position G. Die "Gleichung" G + H + (-H) = G ist daher korrekt, wenn sie als Identität der Gewinnaussichten interpretiert wird.
Erlauben es Milnors Ungleichungen zunächst, die Gewinnaussichten einer Position aus denen ihrer Teilpositionen abzuschätzen, so kann mit Hilfe der Subtraktion von Positionen eine universelle Anwendbarkeit erreicht werden. Sollen nämlich die Gewinnaussichten von zwei beliebigen Positionen G und H miteinander verglichen werden, so geht das mit Milnors Ungleichungen auf der Basis der Differenz-Position G + (-H), kurz G - H. Wegen der Gleichung
G = H + (G - H)
ist innerhalb einer beliebigen Gesamtposition die Teilposition G im Vergleich zur Teilposition H
- mindestens so günstig im Fall von W(G - H) > 0,
- gleich günstig im Fall von W(G - H) = S(G - H) = 0,
- höchstens so günstig im Fall von S(G - H) < 0 bzw.
- je nach Anzugsrecht und restlicher Position mehr, weniger oder gleich günstig im Fall von W(G - H) < 0 < S(G - H).
In einer Partie muß ein Spieler vor jedem Zug die Gewinnaussichten von Positionen miteinander vergleichen. Hat er etwa die Wahl, in einer Position G unter anderem auf die Schnittpunkte x und y zu setzen und dabei die Position Gx beziehungsweise Gy zu erreichen, so sollte er sich für jenen Zug entscheiden, durch den er als Nachziehender den höheren Minimax-Wert erreicht. Da die beiden Positionen Gx und Gy aus derselben Position entstehen, unterscheiden sie sich nur an wenigen Stellen, so daß die Differenz-Position Gx - Gy häufig relativ einfach ist. Ihre beiden Minimax-Werte beinhalten Informationen darüber, welcher der beiden Züge der bessere ist. Als Beispiel nehmen wir eine Position, die die schon untersuchte Position M als Teilposition enthält. Der Sachverhalt, daß es außerhalb der Teilposition noch sinnvolle Züge geben kann, ist im oberen Teil des folgenden Diagramms schematsich dargestellt:
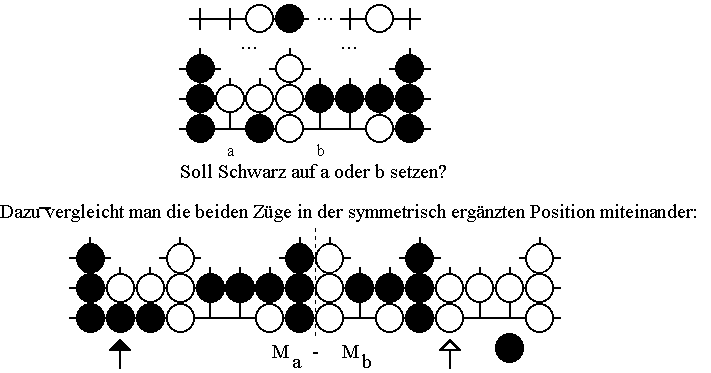
Die außerhalb der Teilposition liegenden Teile des Spielbrettes ergänzen sich innerhalb der abgebildeten Differenz-Position Ma - Mb zu einer Nullposition. Da diese Nullposition die Gewinnaussichten nicht beeinflußt, wurde sie im Diagramm bereits weggelassen. Analysiert man nun die Zugfolgen, wie sie von der abgebildeten Differenzposition aus möglich sind, so erhält man
S(Ma - Mb) = 1 und W(Ma - Mb) = -1.
Damit kann ohne Kenntnis des restlichen Brettes nicht entschieden werden, ob für Schwarz der Zug auf den Schnittpunkt a oder b besser ist. Tatsächlich ist je nach Restposition mal der Zug auf den Schnittpunkt a und mal der Zug auf b besser. Auch wenn dieses Ergebnis hinter den Erwartungen zurückbleiben mag, so zeigt das Beispiel doch recht deutlich, welche Situationen qualitativ möglich sind. Insbesondere sind Züge keineswegs immer lokal vergleichbar! Um das Prinzip noch weiter zu verdeutlichen, sehen wir uns ein weiteres Beispiel an:
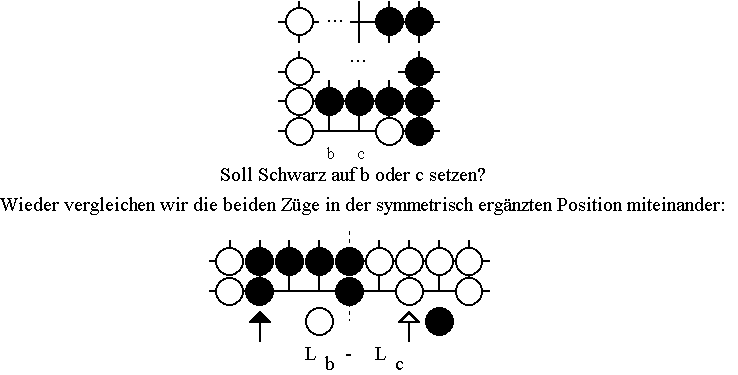
Egal, wer in dieser so entstandenen Position zieht, das Ergebnis beträgt einen Punkt für Schwarz: S(Lb - Lc) = W(Lb - Lc) = 1. Damit wird eindeutig bestätigt, was kein nur etwas erfahrener Go-Spieler anders vermuten würde, nämlich daß für Schwarz der Zug auf den Schnittpunkt b stets besser ist als der auf c.
Wie gut ein Zug ist, kann nicht nur im direkten Vergleich mit einer anderen Zugmöglichkeit untersucht werden. Möglich ist es ebenso, die Positionen nach einem Zug zunächst mit der Position vor dem Zug zu vergleichen. So können insbesondere offensichtlich schlechte Züge direkt ausgeschieden werden. Formal wird dazu wieder eine Differenz-Position gebildet, wobei sich die folgende Vorzeichen-Konvention bewährt hat: Zieht Schwarz von einer Position G zur Position G', nimmt man die Differenz G' - G; zieht dagegen Weiß von der Position G nach G", so bildet man G - G". Die Gewinnaussichten einer solchen, Inzentive oder Anreiz genannten Differenz ist dann ein Maß dafür, wie lohnend der Zug ist. Die Gesamtheit der Inzentives einer Position gibt an, wie wertvoll das Zugrecht ist. Der praktische Nutzen der Inzentives rührt daher, daß bei der Differenz-Bildung die nicht vom Zug betroffenen Teilpositionen wegfallen und dadurch bei unterschiedlichen Positionen oft gleiche Inzentives entstehen. Bei anderen Positionen zuvor gesammelte Erfahrung wird damit leichter übertragbar.
Die bisher vorgestellten Ergebnisse sind aus mathematischer Sicht allesamt nicht sehr tiefliegend. Wen der mathematische Formalismus nicht abschreckt, kann sie im Prinzip nachvollziehen. Außerdem hält sich der spielerische Nutzen bei den untersuchten Beispielen in Grenzen. Trotzdem sind die bisherigen Resultate aus zwei Gründen bemerkenswert: Einerseits ist der Ansatz äußerst originell, da er zeigt, wie Go mathematisch modelliert werden kann. Zum anderen erlauben es die Ungleichungen, einige für Go typische Situationen und Erscheinungen objektiv zu analysieren.
Ausgehend von Milnors Arbeit erzielte der schwedische Mathematiker Olof Hanner 1959 den nächsten Fortschritt. Wieder auf völlig abstraktem Niveau, das heißt ohne das Go-Spiel überhaupt nur zu erwähnen, fand Hanner eine relativ einfach anwendbare Methode, mit der sich für Positionen, die aus mehreren Teilpositionen zusammengesetzt sind, annähernd optimale Ergebnisse erzielen lassen. Das heißt, die so gefundenen Züge sind zwar nicht unbedingt optimal, aber immerhin relativ gut, da der so zu sichernde Gewinn nur wenig unterhalb dem theoretisch bestmöglichen Wert liegt. Möglich ist das, weil sich die Gewinnaussichten einer Position weitgehend durch zwei Maßzahlen charakterisieren lassen, die im Vergleich zu den exakten Minimax-Werten oft einfacher berechenbar sind. Vom Ansatz ist eine solche Konstruktion in der Mathematik keineswegs ungewöhnlich. So ist es in der Wahrscheinlichkeitsrechnung üblich, zufällige Größen wie etwa das Ergebnis eines Würfels ungefähr durch zwei leicht zu handhabende Parameter zu charakterisieren, bei denen es sich um Maße der durchschnittlichen Größe sowie der durchschnittlichen Streuung darum handelt. Im Fall des Go besitzen die von Hanner zu jeder Position G konstruierten Parameter die folgenden Eigenschaften: Die erste Maßzahl ist der sogenannte Mittelwert m(G), der größenmäßig stets zwischen den beiden Minimax-Werten liegt. Wie weit die Minimax-Werten davon höchstens abweichen können, darüber gibt der zweite, Temperatur genannte Parameter t(G) Auskunft. Insgesamt gestalten sich die Größenverhältnisse folgendermaßen:
m(G) - t(G) < W(G) < m(G) < S(G) < m(G) + t(G)
Man sieht, daß sich bei Positionen mit geringer Temperatur die beiden Minimax-Werte nicht stark unterscheiden können, womit der Vorteil des ersten Zuges nicht sehr groß sein kann. Die schon erwähnte Möglichkeit, Mittelwert und Temperatur oft relativ einfach bestimmen zu können, bezieht sich vor allem auf Positionen, für deren sämtliche Teilpositionen die beiden Parameter bekannt sind. Die Mittelwerte der Teilpositionen werden dazu addiert; die Temperatur kann nie die höchste Temperatur einer Teilposition übersteigen:
m(G + H) = m(G) + m(H),
t(G + H) < max(t(G), t(H)).
Wie nützlich die beiden Parameter sind, macht man sich am schnellsten an Hand eines Beispiels klar. Wir greifen dazu auf die bereits eingangs untersuchten Positionen zurück, deren Paramter - wie wir noch sehen werden - die folgenden Werte aufweisen:
m(K) = -1, t(K) = 1
sowie
m(L) = 2, t(L) = 1.
Folglich ergeben sich für die Position M = K + L die Aussagen
m(M) = 1, t(M) < 1.
Auch wenn damit für das Beispiel der Position M die letztlich interessierenden Minimax-Werte nicht exakt bestimmt werden können, so wird besonders im Fall von mehrfachen Summen gut deutlich, wie praktisch Mittelwert und Temperatur sein können. Beispielsweise ist
m(K + K + L + L + L) = 4 und t(K + K + L + L + L) < 1,
woraus die Gewinnaussichten auch dieser umfangreichen Position fast exakt ersichtlich sind, weil die Minimax-Werte beide zwischen 3 und 5 liegen müssen. Daß eine solche Aussage überhaupt möglich ist, liegt daran, daß sich die Vorteile, in einer Position als erster ziehen zu können, bei mehreren Teilpositionen auf beide Spieler verteilen. Besonders interessant ist die Situation, bei der eine beliebige Position G zur n-fachen Summe n×G = G + G + ... + G vervielfacht wird. Diese Summe hat die folgenden Eigenschaften:
m(n.G) = n×m(G),
t(n.G) < t(G),
n×m(G) - t(G) < W(n×G) < n×m(G)
< S(n×G) < n×m(G) + t(G).
Folglich läßt sich der Mittelwert m(G) zumindest theoretisch mit Hilfe der Quotienten W(n×G)/n oder S(n×G)/n näherungsweise bestimmen. Der dabei gemachte Fehler ist höchstens gleich t(G)/n. Selbst wenn man den konkreten Wert der Temperatur nicht kennt, so ist doch stets gesichert, daß der gemachte Fehler beliebig klein wird, wenn die Position G nur genügend oft vervielfacht wird.
Wie aber sind Mittelwert und Temperatur einer Position überhaupt definiert und wie lassen sie sich praktisch berechnen? Hanners Technik basiert auf einer Idee, den mit einem Zug erreichten Vorteil gegen das verlorene Zugrecht abzuwägen. Dazu konstruiert Hanner eine Spielvariante, bei der jeweils ziehende Spieler für seinen Zug einen Betrag an seinen Gegner entrichten muß. Der Anreiz zum Ziehen wird durch diese "Steuer", wie der Betrag später treffend benannt wurde, gedämpft. Je höher die Steuer ist, desto weniger rentabel werden Züge und desto mehr "kühlt" - wie man sagt - das Spiel ab. Interessant wird die Sache dadurch, daß ein Spieler seine Steuer im nächsten Zug des Gegners ganz oder teilweise zurückbekommen kann, da natürlich auch der Gegner besteuert wird. Um realistische Bewertungen des Zugrechts zu erhalten, darf ein Spieler, dem die geforderte Steuer zu erscheint, seinen Gegner um einen Nachlaß ersuchen. Dazu ist er insbesondere dann gezwungen, wenn die Steuerforderung den Vorteil des Zugrechts übersteigt. Dagegen soll eine unbegründete "Steuermüdigkeit" verhindert werden. Konkret soll ein Spieler, dessen Steuer nachgelassen wird, an seinem Zugrecht nichts verdienen. Erreicht wird das mit dem folgenden Verfahren: Der um einen Nachlaß ersuchende Spieler bietet einen Betrag, den er bereit ist, als Steuer zu zahlen, wobei der Gegner das Recht erhält, für eine dieses Angebot übersteigende Steuer als nächster ziehen zu dürfen. Im Vergleich zum Vorteil des Zuges zu niedrige Angebote sind daher nachteilig. Nachdem ein Spieler gezogen hat, kommt sein Gegner zum Zug, wobei als Steuer der zuletzt tatsächlich gezahlte Betrag gefordert wird.
Wie sich die bei der Kühlung zu zahlenden Steuern konkret auswirken, soll an drei Beispielen verdeutlicht werden. Wir beginnen mit der eingangs mit K bezeichneten Position, bei der erste zugleich der letzte Zug ist. Ohne Steuer beträgt der Gewinn für Schwarz als Anziehenden 0 beziehungsweise -2 als Nachziehenden. Wird nun eine Steuer in einer nicht zu großen Höhe t gefordert, so bewegen sich die Minimax-Werte aufeinander zu: Als Anziehender verschlechtert sich das Ergebnis für Schwarz auf -t, als Nachziehender verbessert es sich dafür auf -2 + t, wobei kein Spieler um eine Steuererleichterung bitten wird, weil damit das Recht auf den trotz Steuer noch lukrativen Zug verloren gehen könnte. Das ändert sich erst, wenn eine Steuer von mehr als t = 1 gefordert wird. Dann ist es dem ziehenden Spieler möglich, einen Nachlaß auf die Höhe t = 1 zu erreichen, ohne dabei das Zugrecht zu verlieren. Wie die Gewinnaussichten für Schwarz bei einer Kühlung um t, das heißt bei einer anfänglichen Steuerforderung von t, beeinflußt werden, das zeigt auf einen Blick das folgende Diagramm. Für jede der drei abgebildeten Positionen sind die gekühlten Minimax-Werte dargestellt:
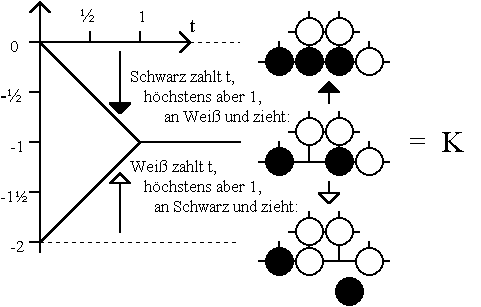
Wie man in der Abbildung deutlich erkennt, fallen die beiden gekühlten Minimax-Werte der Position K zusammen, wenn die anfängliche Steuerforderung 1 oder mehr beträgt. Diese für das Zusammenfallen mindestens erforderliche Steuerforderung wird als Temperatur der Position definiert, also t(K)= 1. Der Wert, den die entsprechend stark gekühlten Minimax-Werte annehmen, ergibt den Mittelwert, das heißt m(K) = -1.
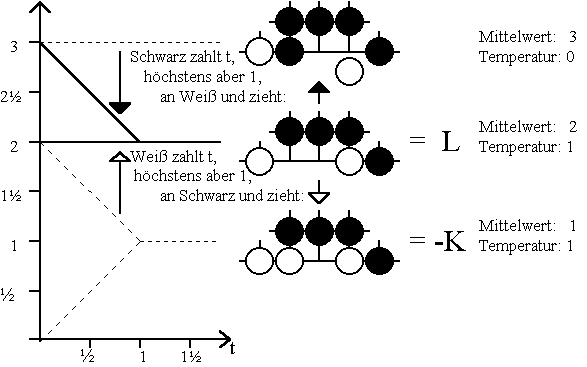
Betrachten wir nun die unter der Bezeichnung L bereits untersuchte Position: Beginnt Schwarz, kann er mit dem ersten Zug den Gewinn von 3 erreichen, was sich nach Steuern auf 3 - t verringert. Macht dagegen Weiß den ersten Zug, entsteht die Position -K, dessen gekühlte Minimax-Werte im folgenden Diagramm gestrichelt dargestellt sind. Wie man im Diagramm erkennt, kann Weiß als Anziehender die Steuer gut verkraften, weil er sie im zweiten Zug von Schwarz zurück erhält. Wieder ist die Temperatur gleich 1; der Mittelwert ist gleich 2:
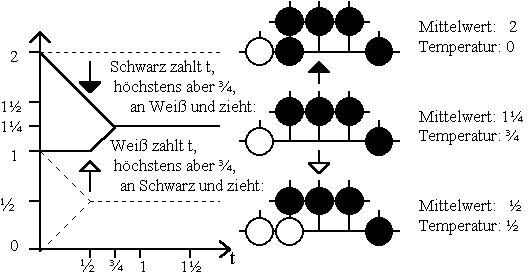
Auch beim letzten Beispiel für die Besteuerung von Minimax-Werte kann Weiß niedrige Steuern problemlos verkraften, da er sie im Zug danach von Schwarz zurück erhält. Das ändert sich allerdings schon dann, wenn die geforderte Steuer ½ übersteigt, da Schwarz im nächsten Zug kaum bereit sein wird, das Zugrecht mit einer ½ übersteigenden Steuer zu sichern. Trotzdem sollte Weiß im ersten Zug Steuern noch bis zur maximalen Höhe von ¾ bezahlen, um den Vorteil des Zugrechtes nicht zu gefährden:
Ein Thermograph, wie die graphischen Darstellung der Minimax-Werte bei variierter Kühlung genannt wird, hat allgemein die folgenden Eigenschaften, die sich Zug für Zug weitervererben:
- Wird genügend stark abgekühlt, das heißt, ist die
anfänglich geforderte Steuer hoch genug, bewirkt das
eine Angleichung der beiden Minimax-Werte, eben auf den
so definierten Mittelwert. Die Höhe der anfänglichen
Steuerforderung, die dazu notwendig ist, wird als
Temperatur definiert.
- Die Schenkel des Thermographen verlaufen waagrecht oder
im 45o-Winkel. Das
bedeutet, daß genügend kleine Erhöhungen der
Steuerforderung einen Spieler entweder voll oder gar
nicht belasten.
- Die Differenz zwischen Mittelwert und einem unbesteuerten
Minimax-Werte kann daher nie größer als die Temperatur
sein.
- Milnors Ungleichungen lassen sich auf gekühlte Minimax-Werte verallgemeinern:
Wt(G) + Wt(H) < Wt(G + H) < Wt(G) + St(H)
St(G) + Wt(H) < St(G + H) < St(G) + St(H)
- Kennt man die Thermographen aller Teilpositionen einer gegebenen Gesamtposition, so können mit einem relativ einfachen Verfahren annähernd optimale Strategien gefunden werden. Dabei wird meistens in der heißesten Teilposition gezogen und zwar so, als wäre der Rest nicht vorhanden. Wird diese Technik von Schwarz als Anziehendem durchgehend verwendet, so sichert er sich damit mindestens die Summe der Mittelwerte. Im Nachzug ist der für Schwarz bei dieser Strategie garantierte Gewinn etwas kleiner, wobei der Abschlag geringer als die höchste Einzeltemperatur ausfällt.
Wird die als letztes Beispiel untersuchte Position vervielfacht, können ihre Gewinnaussichten sofort angegeben werden. So besitzt beispielsweise die Position

den Mittelwert 3¾ und eine Temperatur von höchstens ¾. Da die Minimax-Werte ganze Zahlen sind, beträgt der Punktgewinn für Schwarz bei beidseitig optimalem Spiel 4 als Anziehender beziehungsweise 3 als Nachziehender. Bei der vervierfachten Position

sind hingegen beide Minimax-Werte gleich deren Mittelwert 5, weil um diesen im Abstand der Temperatur von höchstens ¾ keine andere ganze Zahl liegt.
Bei der nächsten Position, die zusammen mit den Mittelwerten und Temperaturen ihrer Teilpositionen abgebildet ist, handelt es sich um eine Nullposition:

Wie schon erwähnt, erfolgten die Untersuchungen von Milnor und Hanner auf einem sehr abstrakten Niveau. Auf das Go angewendet - so wie hier soeben beschrieben - wurden sie erstmals 1991 von Elwyn Berlekamp, einem an der Universität von Kalifornien tätigen Experten für Kodierungstheorie. Dazwischen liegt die Entstehung der kombinatorischen Spieltheorie (siehe Kasten), die Berlekamp und seinem Doktoranden David Wolfe als mathematisches Fundament ihrer Untersuchung diente. Als spielerische Grundlage kreierten sie das Mathematische Go, ein dem Go sehr ähnliches Spiel, bei dem der zuletzt ziehende Spieler gewinnt und dessen Gewinnaussichten dem des Go äquivalent sind.
| Kombinatorische Spieltheorie Anders als ihr Name vermuten läßt, ist die kombinatorische Spieltheorie eigentlich kein Bestandteil der klassischen, auf ökonomische Modellbildungen orientierten Spieltheorie. Im Mittelpunkt der kombinatorischen Spieltheorie steht weniger der Gewinn eines Spieles und schon gar nicht seine Höhe, sondern vielmehr die Art, wie sich die Zugmöglichkeiten zu Partien kombinieren können. Untersucht werden dabei zufallsfreie Zweipersonen-Spiele, deren aktuelle Position stets beiden Spielern bekannt ist. Formal wird eine Position durch die Angaben darüber bestimmt, zu welchen Positionen von ihr aus der eine Spieler ziehen kann und zu welchen der andere. Verloren wird eine Partie von dem Spieler, der als erster nicht mehr ziehen kann - seltener wird nach der dazu umgekehrten Regel gespielt. Als erstes Spiel in diesem Sinne wurde das sogenannte Nim-Spiel 1902 von Charles Bouton untersucht: Gespielt wird mit Steinen, die zu mehreren Haufen gruppiert sind. Jeder Spieler muß in seinem Zug einen Haufen aussuchen und dort mindestens einen Stein - ganz nach Wunsch auch mehr - wegnehmen. Bouton fand eine einfache Formel, mit der ein auf Gewinn stehender Spieler sofort einen entsprechenden Gewinnzug finden kann. Da die Formel das binäre Zahlensystem verwendet, konnte bereits 1940 eine Maschine auf der New Yorker Weltausstellung vorgestellt werden, die Nim fehlerfrei spielte. Gewinnstrategien für Varianten des Nim fanden in der zweiten Hälfte der dreißiger Jahre unabhängig voneinander Roland Sprague und Patrick Michael Grundy, nachdem bereits Lasker im eingangs zitierten Buch einige Grundideen skizziert hatte. Wesentlicher Bestandteil der Theorie sind Methoden, mit denen die Gewinnaussichten von zusammengesetzten Positionen aus Daten der Teilpositionen bestimmt werden können. Bei Nim und seinen Varianten sind die Zugmöglichkeiten unabhängig davon, wer zieht. Diese für gebräuchliche Spiele eher ungewöhnliche Einschränkung beseitigte zu Beginn der siebziger Jahre der durch seine Beiträge sowohl zur Gruppen- als auch Knotentheorie bekannte Mathematiker John Horton Conway. Seine Theorie offenbart bemerkenswerte Beziehungen zwischen Zahlen und Spielen. Zahlen, sowohl die üblichen wie 3, -5, 1¾ und p2 als auch solche, die man als unendlich groß oder klein interpretieren kann, erscheinen in Conways Theorie als Spezialfälle von Spielen. Dabei kann der Größenvergleich zwischen Zahlen als Vergleich von Gewinnaussichten und die Addition als Nebeneinanderlegen von Positionen gedeutet werden. Zusammen mit seinen Kollegen Richard Guy und Elwyn Berlekamp verfaßte Conway zu diversen Spielen seitdem umfangreiche Studien - viele davon sind zu finden in denen ins Deutsche übersetzten Büchern "Gewinnen" und "Über Zahlen und Spiele". So verspielt diese Bücher mit ihren zum Teil witzigen Graphiken auch scheinen mögen, so sehr ist ihr Inhalt doch mathematisch geprägt und für den Laien oft keineswegs einfach zu verstehen. Spiele der von Conway untersuchten Art werden wie Nim von demjenigen Spieler gewonnen, dem es gelingt, als letzter zu ziehen. Zu Zweipersonen-Spielen mit Punktwertung bestehen allerdings enge Beziehungen, die 1991 von Berlekamp dazu verwendet wurden, das Go-Spiel zu untersuchen. Dazu transfomierte Berlekamp die verschiedenen Go-Varianten unter der Sammelbezeichnung "Mathematisches Go" in äquivalente Conway-Spiele, um so die zahlreichen Ergebnisse aus der kombinatorischen Spieltheorie auf Go anwenden zu können. Folglich sind Berlekamps Arbeiten voll mit Symbolen wie ¬, , ¯ und +2, die allesamt bereits von Conway untersuchte Spiele bezeichnen. Beim Mathematischen Go entstehen sie, wenn dessen Positionen um 1 abgekühlt werden. |
Eine zentrale Idee Berlekamps besteht darin, Go-Positionen abzukühlen. Gleichsam wie mit einer technischen Zeichnung, die bestimmte Eigenschaften aus einer günstig gewählten Perspektive hervorhebt, gelingt es ihm damit, einige unwesentliche Details auszublenden und so die eigentlich interessierenden Gewinnaussichten einfacher zu erkennen. Konkret kühlt Berlekamp die Positionen um 1 ab - allerdings die Positionen des von ihm untersuchten Mathematischen Go, wobei er sogar auf Steuererleichterungen zugunsten geringfügiger Korrekturen des Endergebnisses verzichten kann. Wieso in Berlekamps Mathematischen Go gerade die Abkühlung um 1 so interessant ist, wird plausibel, wenn man im normalen Go die Minimax-Werte um etwas weniger als 1 abkühlt:
- Da sich die Minimax-Werte bei der Kühlung um jeweils weniger als 1 aufeinander zubewegen und die originalen Minimax-Werte ganze Zahlen sind, sind diese aus den Daten des gekühlten Spieles ablesbar. Sogar gute Züge können innerhalb dieser gekühlten Variante gefunden werden. Betrachtet man nämlich die während einer Zugfolge gezahlten Steuern, so werden deren Beträge nie größer, so daß sich die wechselseitigen Zahlungen fast kompensieren, das heißt, ihr Saldo ist für den beginnenden Spieler höchstens gleich 0 und größer als -1. Kluge Strategien eines Spielers innerhalb der gekühlten Variante, die den dortigen Minimax-Wert sichern, können daher mit Erfolg ins normale Spiel übertragen werden, weil sie dort ebenso optimal sind.
- Aufgrund der Kühlung vereinfachen sich viele Positionen
und Zugvarianten, da jede Position mit einer Temperatur
von weniger als 1 auf ihrem Mittelwert
"einfriert". So kann zum Beispiel die schon
untersuchte Position
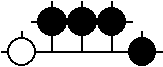
als Teilposition innerhalb einer umfangreicheren Position zunächst wie ein fester Gewinn von 1¼ Punkten für Schwarz angesehen werden. Die Zugmöglichkeiten darin müssen erst wieder in Betracht gezogen werden, wenn es in den anderen Teilpositionen der gekühlten Versionen keinen Anreiz mehr zum Ziehen gibt.
Zum Schluß noch zwei Beispiele etwas komplizierterer Positionen:
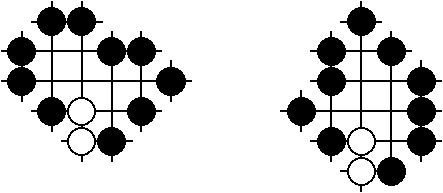
Die linke Position hat, wie Berlekamp und Wolfe in ihrem Buch angeben, einen Mittelwert von 23/8 und eine Temperatur von 17/8. Bei der rechten Position können im weiteren Spielverlauf Kos auftreten, was ihre Analyse stark erschwert. Ein Ansatz, überhaupt Ergebnisse zu erhalten, besteht darin, zwei Regel-Varianten zu untersuchen, in denen jeweils ein Spieler bei den Kos betreffenden Zügen eingeschränkt wird. Bezogen auf die Gewinnaussichten bilden diese beiden Varianten dann eine Eingrenzung der gegebenen Position, das heißt, im Vergleich zu den normalen Regeln ist eine Variante für Schwarz mindestens so günstig, die andere höchstens so günstig. Im vorliegenden Fall ergibt sich, wie Martin Müller von der ETH Zürich in seiner Dissertation aus dem Jahre 1995 ausführt, für die Varianten einmal der Mittelwert 213/32 und die Temperatur 121/32 und das andere Mal der Mittelwert 212/32 und die Temperatur 120/32.
Für Verbesserungsvorschläge zu einer ersten Version dieses Manuskriptes bedankt sich der Autor bei Horst Timm und Martin Müller.
Eine ausführliche Einführung in die kombinatorische Spieltheorie, deren Anwendung auf Go und andere
Spiele enthält mein Buch
Jörg Bewersdorff, Glück, Logik und Bluff: Mathematik im Spiel: Methoden, Ergebnisse und Grenzen,
3. Auflage, Wiesbaden 2003 (Vieweg-Verlag), 363+xiv Seiten, ISBN 3-528-26997-9.
Darin enthalten sind auch zahlreiche Verweise auf die einschlägige Forschungsliteratur. Neben
kombinatorischen Spielen werden Glücksspiele, strategische Spiele sowie deren Mathematik behandelt.
Einführung, Inhalt und Stichwortverzeichnis
Preface, contents and index of the
English edition Luck, Logic and White Lies: The Mathematics of Games